You are here: Accueil» SPE NSI» Représentation des données

Représentation des données

I - Types et valeurs de base

Ecrire un nombre entier

Ecrire un nombre entier

1- Quelle différence entre un chiffre et un nombre ?
Un chiffre est un symbole pour représenter un nombre.
Exemple : (2345)occidental = (٢٣٤٥)arabe = (MMCCCXLV)romain = 二三四五(coréen)
Un nombre peut donc être représenté de différentes manières, cependant à l'exception de la notation romaine, les 3 autres exemples se basent sur une méthode commune : la notation en base 10 ou décimale.
Cette façon de représenter les nombres se base sur la décomposition en puissances de 10. Ainsi le nombre deux-mille-trois-cent-quarante-cinq se note usuellement 2345 car :
2345=2×1000 + 3×100 + 4×10 + 5×1
2345=2×103+3×102+4×101+5×100.
2- Comment écrire un nombre dans une autre base que 10 ?
Il est parfaitement possible d'écrire un nombre dans une autre base que 10, il est cependant évident qu'il ne sera pas formé des mêmes chiffres. Pour ne pas être induit en erreur par la base dans laquelle est exprimée un nombre, on écrit le nombre entre parenthèses avec en indice le nombre correspondant à la base dans lequel il est écrit : (100)10 est le nombre s'écrivant un-zéro-zéro en base dix, il s'agit donc de cent. En revanche le nombre (100)8 est le nombre s'écrivant un-zéro-zéro en base huit (octal) qui correspond au nombre soixante-quatre !

La base la plus simple imaginable est le binaire, où un nombre se décompose en puissances de 2 successives et ne s'écrit donc qu'avec 2 chiffres différents : 0 et 1.
a. Convertir le nombre (343)5 en décimal :
(343)5=3×52+4×51+3×50
(343)5=3×25+4×5+3×=75 + 20 + 3=98
b. Convertir le nombre (343)10 en octal :
La démarche est un peu différente, du fait que la base 10 est notre base usuelle. On commence par lister les différentes puissance de la base d'arrivée : 80=(1)10 ; 81=(8)10 ; 82=(64)10 ; 83=(512)10 ; 84=(4096)10.
On voit que (343)10<(512)10, ce nombre s'écrira donc avec 3 chiffres en base 8.
(343)10=5×64+23
23=2×8+7
7=7×1
Ainsi (343)10 = 5×82+2×81+7×80

On a donc (343)10 = (527)8.
Et pour les bases > 10 ?
Dans ce cas, nous utilisons comme chiffres supplémentaires les lettres de l'alphabet :
0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; A ; B ; C ; D ; E ; F ...
La base la plus courante en informatique après le binaire est l'hexadécimal ou base 16. On utilise pour représenter les nombres dans cette base les chiffres de 0 à F [c'est à dire (15)10].
a. Convertir le nombre (2A3)16 en décimal :
(2A3)16=2×162+A×161+3×160
(2A3)16=2×256+10×16+3×=(675)10
b. Convertir le nombre (343)10 en hexadécimal :
On commence par lister les différentes puissance de la base d'arrivée : 160=(1)10 ; 161=(16)10 ; 162=(256)10 ; 163=(4096)10.
On voit que (343)10<(4096)10, ce nombre s'écrira donc avec 3 chiffres en base 16.
(343)10=1×256+87
87=5×16+7
7=7×1
Ainsi (343)10 = 1×162+5×161+7×160

On a donc (343)10 = (157)16.
3 - Les exercices
Application : Réussir au moins 6 fois d'affilée chaque exercice
  1. Écrire le nombre indiqué dans la base décimale :
    (XXX)XXX=()10.
     Réussite(s) successive(s):0
  2. Écrire le nombre dans la base indiquée :
    (XXX)10 = ()XXX.
     Réussite(s) successive(s):0
4 - Opérations mathématiques
Regarder la vidéo récapitulative suivante :
Remarques : dans n'importe quelle base,
  • La somme de 2 nombres s'écrit au maximum avec un chiffre de plus que le plus grand des deux nombres.
  • Le produit de 2 nombres s'écrit au maximum avec autant de chiffres que la somme des chiffres de chaque nombre.
En base 10, le plus grand nombre à 3 chiffres est 999 et 9999 est le plus grand à 4 chiffres.
  • 999+9999=10998 --> la somme s'écrit avec 4+1=5 chiffres.
  • 999×9999=9989001 --> le produit d'écrit avec 4+3=7 chiffres.

Représentation des nombres en binaire

Représentation des nombres en binaire

Le binaire étant la base numérique par excellence de l'informatique, on s'intéresse maintenant à la façon dont on peut écrire n'importe quel nombre.
1 - Nombre de bits nécessaires
Certains langages informatiques nécessitent de connaître à l'avance valeur maximale des nombres que l'on va manipuler. En effet, cela leur permet d'allouer préventivement la place nécessaire en mémoire.
Pour les entiers naturels, sur n bits, il est possible d'encoder 2n nombres, soit les nombres allant de 0 jusqu'à 2n-1
En considérant chaque doigt de nos 2 mains comme un bit de donnée, un doigt fermé représentant 0 et un doigt levé représentant 1, il est possible de former tous les nombres compris entre (00000 00000)2 = (0)10 et (11111 11111)2=(1023)10=210-1.
Exercice :
Préciser sur combien de bits au minimum il est possible de coder les nombres suivants en binaire : 5, 32, 127, 554, 10 235 468
On utilise usuellement en informatique des longueurs multiples de 8 bits (1 octet)
Anecdote : J'ai codé un Tetris® pour arduino il y a quelques années. J'avais utilisé par défaut des nombres de 16bits pour toutes mes variables. Impossible de compiler le programme car il nécessitait trop de mémoire. En limitant la taille des variables au strict nécessaire, le programme fonctionne !
10 - Nombres négatifs
Le binaire n'est qu'une succession de 0 et de 1, il n'est donc pas possible d'ajouter un signe "-" devant un nombre binaire pour signifier que celui-ci est négatif.
Une fois que le nombre de bits sur lequel va être encodé le nombre est défini, on utilisera le premier bit pour indiquer si ce nombre est positif ou négatif.
Si l'on souhaite encoder le nombre (23)10 sur 8bits, alors on pourrait écrire (23)10=(0000010111)2 et (-23)10=(1000010111)2. Cette possibilité pourrait être envisageable, mais a un énorme inconvénient : les règles de l'addition ne fonctionnent alors plus.
On utilise donc une méthode qui permettra de conserver le fonctionnement classique de l'addition : Le complément à 2
Pour représenter un nombre négatif, on code le nombre positif en binaire, on inverse ses chiffres (0 devient 1 et 1 devient 0) puis on ajoute 1, sans tenir compte du dépassement.
  1. Je veux coder (-23)10 sur 8 bits :
    (23)10=(00010111)2
    On inverse les bits : (00010111)2 → 11101000
    On ajoute 1 : 11101000 + 1 → 11101001=(-23)10
  2. Je veux trouver le positif de (11101001)2 :
    On inverse les bits : (11101001)2 → 00010110
    On ajoute 1 : 00010110 + 1 → 00010111=(23)10
  3. Je veux coder (-157)10 sur 8 bits :
    (157)10=(10011101)2 ✖ le bit de signe est déjà à 1, ce qui signifie que ce nombre sur 8 bits devrait déjà être considéré comme négatif !
Si on dispose de n bits pour coder des entiers relatifs, alors il sera possible d'utiliser les entiers compris entre -2n-1+1 et 2n-1-1
Pour reprendre l'exemple précédent, sur 8 bits, on peut coder les nombres compris entre -2n-1+1 =-27+1 = -127 et 2n-1-1 = -27+1 = 127.
Application : Réussir au moins 3 fois d'affilée chaque exercice
  1. Écrire le négatif de cet entier relatif binaire codé sur 8 bits:
    XXX→.
     Réussite(s) successive(s):0
  2. Convertir l'entier relatif suivant codé sur 8 bits dans la base décimale :
    (XXX)2 = ()10.
     Réussite(s) successive(s):0
11 - Les nombres réels
Il est également possible de trouver un moyen de coder un nombre réel en binaire. On commence par coder la partie entière, puis ensuite on code la partie fractionnaire selon la méthode suivante :
On souhaite coder (23,375)10 = (23)10 + (0,375)10
  • La partie entière : (23)10=(10111)2
  • Pour la partie fractionnaire, il faut réaliser des multiplications par 2 successives. Si le résultat est supérieur à 1, alors on ajoute un 1 dans la partie fractionnaire binaire, sinon on ajoute 0 :
    0.375×2=0.75 → on ajoute 0
    0.75×2=1.5 → on ajoute 1
    0.5×2=1.0 → on ajoute 1
    On s'arrête ici puisqu'il n'y a plus de reste.
    On a donc (23,375)10=(10111,011)2
    • Application : Réussir au moins 3 fois ces exercices
    1. Convertir le nombre suivant en binaire :
      (XXX)10→()2.
       Réussite(s) successive(s):0
    2. Convertir le nombre binaire suivant en décimal :
      (XXX)2→()10.
       Réussite(s) successive(s):0
    La méthode précédente n'est en fait que la prolongation de l'écriture binaire :
    (21.4375)10=2×101+2×100+4×10-1+3×10-2+7×10-3+5×10-4
    (21.4375)10=(10101.0111)2=1×24+0×23+1×22+0×21+1×20+0×2-1+1×2-2+1×2-3+1×2-4
    Remarque : Tout comme il n'est pas toujours possible d'écrire exactement un nombre en base 10 (1/3=0.3333333... ou π=3.141592....), certains nombres ne peuvent pas être écrits exactement en binaire.
    Le langage javascript que j'utilise pour écrire les appplication de ce cours code les nombres dans un format que nous évoquerons plus bas, mais qui permet d'afficher jusqu'à 16 chiffres significatifs.
    Testez ci-dessous l'ecriture binaire du nombre réel décimal de votre choix :
    ()10→(XXX)2.
    Le nombre décimal qui correspond en réalité à ce nombre binaire est : (__)10
    Il faut être conscient qu'un nombre réel écrit en base 10, ne sera pas forcément traité à l'identique par la machine qui utilisera elle une notation binaire qui ne tombera pas forcément "juste".
    Conséquence : Dans un programme, il faut éviter d'utiliser des comparaisons Si A=B, alors... si A et B ne sont pas des nombres entiers !
    A essayer avec votre interpréteur Python :
    • Le problème de la soustraction :
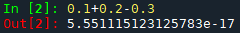
    • Le problème d'une comparaison dans un programme :
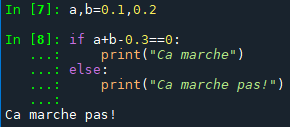
    100 - Ecrire un nombre réel en binaire
    Pour travailler avec des nombres qui peuvent être à la fois très grands et très petits, le plus simple est d’utiliser un analogue de la notation scientifique.
    Un nombre sera écrit sous la forme x = s × m × 2exp
    Avec s qui correspond au signe, m appelé mantisse (0< m < 1),et exp, l’exposant.
    Exemple : (25,32)10 = 0,2532 × 102 (-0,065)10 = – 0,0065 × 10-3
    7. Écrire sous la forme précédente le nombre (7,625)10 puis tenter de l’écrire sous forme binaire.
    Pour coder un nombre flottant sur 1 octet, on utilisera 1bit de signe, 3bits d’exposant et 4 bits de mantisse :
    +1101,1 = + 1,1011 × 23 – 10,0101= – 1,00101 × 21
    +1101,1 = + 1,1011 × 23   – 10,0101= – 1,00101 × 21
    0011101110010010
    En respectant l’exemple ci-dessus, écrire (-10,125)10 en flottant sur 1 octet. Écrire ensuite ce code en hexadecimal

    Les booléens

    Les booléens

    1 - Vrai ou Faux ?
    Regarder cette vidéo en introduction :
    L'agèbre de Boole permet de traiter des raisonnements logiques comme des opérateurs mathématiques.
    Une variable booléenne est soit vraie soit fausse.
    Par défaut, on code le "vrai" par 1 et le "faux" par 0 (mais rien n'epmêche de choisir l'inverse).
    2 - Les opérateurs booléens
    "Je te paierai ton permis si tu as la moyenne en maths et que tu arrêtes de laisser traiter tes vêtements dans toute la maison"
    Cette phrase contient 3 propositions :
    • A : "Je te paierai ton permis"
    • B : "Tu as la moyenne en maths"
    • C : "Tu arrêtes de laisser trainer tes vêtements dans toute la maison"
    La proposition A n'est vraie que si les propositions B et C le sont également
    Les opérateurs booléens correspondent aux relations qui doivent exister entre différentes propositions pour qu'une autre proposition soit vérifiée ou non.
    Il en existe 3 : "et", "ou", "non" ("and", "or", "not") qu'il est possible de combiner à l'aide de parenthèses.
    On dispose d'un récipient contenant des billes de toutes les couleurs, translucides ou opaques.
  • On souhaite programmer un automate qui ne récupérera que les billes translucides rouges. Pour cela la variable ACCEPTABLE est définie. Le programme serait :
    ACCEPTABLE = TRANSLUCIDE ET ROUGE
  • Si ce robot doit maintenant enlever l'ensemble des billes opaques et des billes bleues, on modifiera le programme en :
    ACCEPTABLE = (NON TRANSLUCIDE) OU BLEUE
    • Dans l'exemple ci-dessus, vous remarquez la présence des parenthèses pour indiquer que l'opérateur NON ne s'applique qu'à translucide et pas NON (TRANSLUCIDE OU BLEUE).
    Quelles seraient les billes ramassées dans ce cas ?
    3 - Table de vérité
    La table de vérité récapitule les résultats différents d'une opération booléenne en fonction des valeurs des variables d'entrée.
    Opérateur "and"
    C = A and B
    A
    01
    B000
    101
    		 Opérateur "or"
    C = A or B
    A
    01
    B001
    111
    		 Opérateur "xor"
    C = A xor B
    A
    01
    B001
    110
    L'opérateur ou exclusif (xor) est souvent utilisé en logique mais il est construit à partir des 3 opérateurs de base : C = A xor B = ( A and ( not B ) ) or ( ( not A ) and B )
    Les circuits informatiques ne sont que assemblages de portes logiques, des dispositifs électroniques ayant pour but de fonctionner comme un opérateur logique.
    Une addition en binaire peut se réaliser à l'aide de portes logiques.

    Coder un texte

    Coder un texte


    Encoder un texte

    Entrez un texte :
    Le code décimal des caractères que vous avez entrés est : ___.
    Le code binaire des caractères que vous avez entrés est : ___.
    Le code hexadécimal des caractères que vous avez entrés est : ___.

     

    Décoder un texte

    Entrez votre code en décimal (séparer les valeurs par un espace) :

    Entrez votre code en hexadécimal (séparer les valeurs par un espace) :

    Entrez votre code en binaire (séparer les groupes d'octets par un espace) :


    Les caractères correspondants sont : .

    II - Types construits

    Les p-uplets

    Les p-uplets

    Lorsque l'on souhaite stocker plusieurs informations dans un même objet, on peut voir que le langage python propose plusieurs possibilités :
    >>> a=(1,2,3)
>>> type(a)
<class 'tuple'>
>>> b=[1,2,3]
>>> type(b)
<class 'list'>
>>> c={"un":1,"deux":2,"trois":3}
>>> type(c)
<class 'dict'>

    1- Les tuples et les listes

    Ces deux objets se ressemblent, la façon de les définir est similaire si ce n'est qu'un tuple s'écrit avec des parenthèses et qu'une liste s'écrit avec des crochets
    a. Lire un tuple ou une liste
    >>> a=(17,23,48,12,54)
>>> len(a)
5
>>>a[2]
48
>>>a[0]
17
>>>a[5]
Traceback (most recent call last):
  File "", line 449, in runcode
  File "", line 1, in 
IndexError: tuple index out of range
    		 
    >>> b=[32,41,76,82,37]
>>> len(b)
5
>>>b[2]
76
>>>b[0]
32
>>>b[5]
Traceback (most recent call last):
  File "", line 449, in runcode
  File "", line 1, in 
IndexError: list index out of range
  • Le nombre d'items contenus dans une liste est donné par la fonction len( ).
  • Pour accéder à un élément en particulier, on utilise le nom de la liste/du tuple suivi du numéro d'index correspondant à l'item désiré, écrit entre crochets.
  • Attention : l'index commence à 0 : L[2] fait donc référence à l'item en 3ème position de la liste (ou du tuple L) !
  • En python il est possible d'accéder directement aux derniers éléments : L[-1] correspond au dernier item de la liste L, L[-2] l'avant-dernier, etc.
    Dans d'autres langages, on est contraint d'utiliser préalablement la longueur de la liste : L[len(L)-1].
    • b. Modifier un tuple ou une liste
    Il n'est pas possible de modifier un item d'un tuple, on dit qu'il est non mutable
    >>> b=[17,23,48,12,54]
>>> b[2]=5
>>> b
[17, 23, 5, 12, 54]
    		 
    >>> a=(17,23,48,12,54)
>>> a[2]=5
Traceback (most recent call last):
  File "", line 449, in runcode
  File "", line 1, in 
TypeError: 'tuple' object does not support item assignment
    c. opération sur les tuples et les listes
  • La concaténation 
    >>> b=[17,23,48,12,54]
>>> b+2
Traceback (most recent call last):
  File "", line 449, in runcode
  File "", line 1, in 
TypeError: can only concatenate list (not "int") to list
>>> b+[2,3]
[17, 23, 48, 12, 54, 2, 3]
>>> b+(3,4)
Traceback (most recent call last):
  File "", line 449, in runcode
  File "", line 1, in 
TypeError: can only concatenate list (not "tuple") to list


    >>> a=(17,23,48,12,54)
>>> a+2
Traceback (most recent call last):
  File "", line 449, in runcode
  File "", line 1, in 
TypeError: can only concatenate tuple (not "int") to tuple
>>> a+(2,3)
(17, 23, 48, 12, 54, 2, 3)
>>> a+[3,4]
Traceback (most recent call last):
  File "", line 449, in runcode
  File "", line 1, in 
TypeError: can only concatenate tuple (not "list") to tuple
    On voit ici que l'opérateur "+" ne symbolise pas l'addition mais la concaténation : il colle la seconde opérande à la suite de la première.
    il n'est pas possible de concaténer des items de types différents.

  • La multiplication 
    >>> b=[17,23,48,12,54]
>>> b*2
[17, 23, 48, 12, 54, 17, 23, 48, 12, 54]

    >>> a=(17,23,48,12,54)
>>> a*2
(17, 23, 48, 12, 54, 17, 23, 48, 12, 54)
    On voit ici que l'opérateur "*" ne multiplie pas chaque item de la liste/tuple comme on pourrait s'y attendre, mais réplique la liste le nombre de fois indiqué

  • Conversion liste <--> tuple 
    >>> b=[17,23,48,12,54]
>>> tuple(b)
(17, 23, 48, 12, 54)

    >>> a=(17,23,48,12,54)
>>> list(a)
[17, 23, 48, 12, 54]
    • d. remplir une liste
    Il existe plusieurs façon de remplir une liste initialement vide
    On souhaite remplir une liste L initialement vide avec les 10 premiers nombres paires (0 inclus) de façon récursive.
    1. par concaténation
    L=[]
for i in range(10):
  L=L+[2*i]
    2. Avec .append( )
    L=[]
for i in range(10):
  L.append(2*i)
    3. Liste en compréhension
    L=[2*i for i in range(10)]
    La dernière méthode est la plus élégante, mais n'est en fait qu'un condensé des deux méthodes précédentes.
    Générer à l'aide d'une des 3 méthodes précédentes les listes suivantes :
    1. A est la liste des 10 premiers entiers
    2. B est la liste des 10 premier entiers strictement positifs
    3. C est la liste des 10 premiers carrés (C=[0,1,4,9,16,25,...])
    4. D est la liste des 10 premiers nombres impairs
    Il est également possible d'utiliser des conditions :
    On souhaite remplir une liste L initialement vide avec les premiers nombres paires inférieurs strictement à 20 qui ne sont pas divisibles par 3 de façon récursive.
    1. par concaténation 2. En compréhension 
    L=[]
for i in range(10):
  if i%3 != 0:
    L=L+[2*i]
    		 
    L=[2*i for i in range(10) if i%3 != 0]

    Les dictionnaires

    Les dictionnaires

    Lors de l'introduction de la partie précédente, nous avons vu cet exemple 
    >>> c={"un":1,"deux":2,"trois":3}
>>> type(c)
<class 'dict'>
    Imaginons que nous souhaitions l'utiliser pour constituer un annuaire téléphonique :
    >>> annuaire={"Pierre":"0601020304","Samia":"0708091011","Kevin":"0605040302"}
>>> annuaire["Samia"]
'0708091011'
>>> annuaire["Gertrude"]="0613141516"
>>> annuaire["Gertrude"]
'0613141516'
>>> annuaire.keys()
dict_keys(['Kevin', 'Gertrude', 'Pierre', 'Samia'])
    On voit ainsi comment créer un dictionnaire, ajouter une clé (key) et comment obtenir la liste des clés contenues dans le dictionnaire
    On souhaite maintenant chercher qui a pour numéro de téléphone "0605040302" :
    On crée le script suivant (fenêtre du haut dans edupython): 
    repertoire={"Pierre":"0601020304","Samia":"0708091011","Kevin":"0605040302","Gertrude":"0613141516"}

def recherche(annuaire,numero):
    for cle in annuaire.keys():
        if annuaire[cle]==numero:
            print("Le numéro",numero,"appartient à",cle)
            return cle
    else :
        print("Ce numéro n'est pas dans l'annuaire")
        return False

    On execute le script (bouton ▶), et la fonction recherche( ) est maintenant active :
    *** Console de processus distant Réinitialisée *** 
>>> recherche(repertoire,"0601020304")
Le numéro 0601020304 appartient à Pierre
'Pierre'
>>> recherche(repertoire,"0601020305")
Ce numéro n'est pas dans l'annuaire
False
    Previous page: SPE NSI Next page: Introduction au langage python