You are here: Accueil» Anciens programmes » 4eme » Les lois du courant continu

Les lois du courant continu

1- Mesurer des grandeurs électrique

a. Fonctionnement d'un multimètre

Un multimètre permet de mesurer, comme son nom l’indique, plusieurs grandeurs électriques :
  • les tensions : elles s’expriment en volt (symbole V),
  • les intensités : elles s’expriment en ampère (symbole A),
  • les résistances : elles s’expriment en ohm (symbole Ω).

Un multimètre a donc trois fonctions :

  • la fonction voltmètre : elle permet des mesures de tension en courant continu et en courant alternatif. En classe de quatrième, toutes les mesures seront faites en courant continu.
  • la fonction ampèremètre,
  • la fonction ohmmètre

 

Pour choisir la fonction de l’appareil, il faut :

  • positionner le sélecteur dans le secteur approprié,
  • repérer la borne d’entrée du courant (rouge ou jaune) et la borne de sortie qui est toujours identifiée par « COM ».

Le calibre correspond à la valeur maximale que peut mesurer l’appareil sans être détérioré. Pour faire une mesure dont on ne connaît pas l’ordre de grandeur, on commence toujours par le calibre le plus élevé. Le passage sur un calibre inférieur, quand il est possible, permet d’améliorer la précision de la mesure.

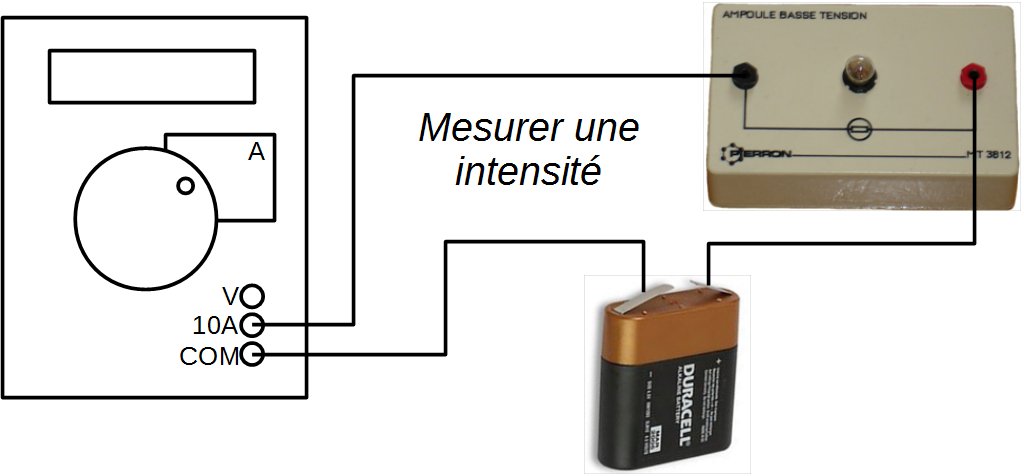
Questions :

  • Quelle grandeur électrique s'apprête-t-on à mesurer avec l'appareil ci-contre ? Justifie ta réponse.
  • En quelle unité faudra-t-il exprimer le résultat de la mesure ?
  • Quelle est la valeur maximale de la mesure réalisable ? Justifie ta réponse.

Réponse :

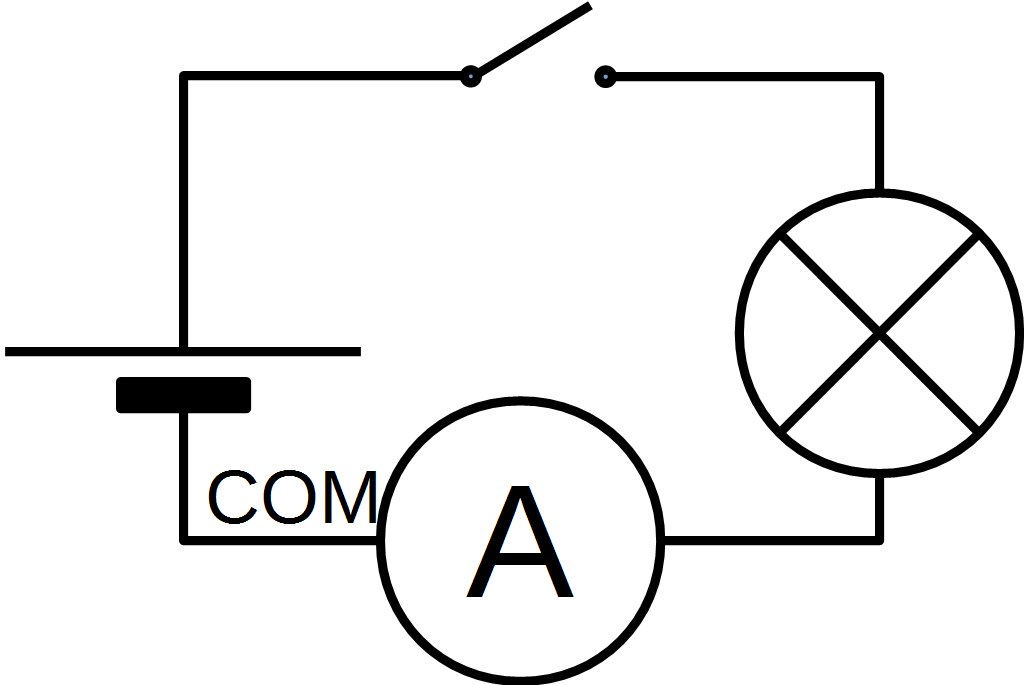
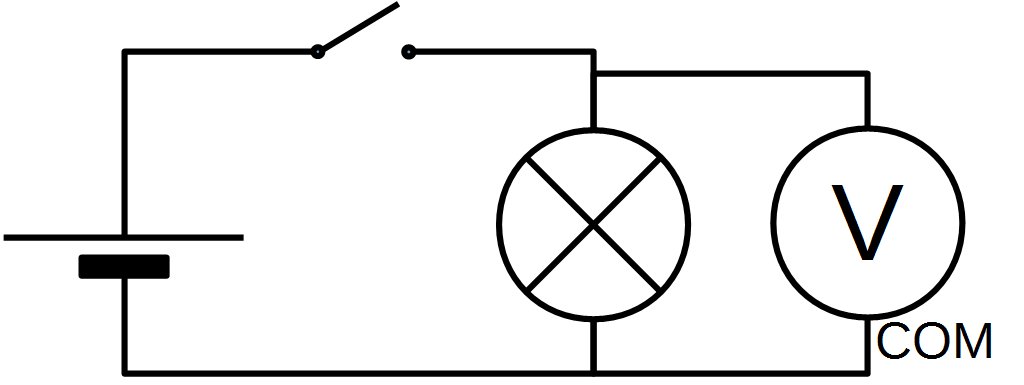
b. Brancher un multimètre dans un circuit

Un multimètre se branche de façon différente dans un circuit selon qu'on désire l'utiliser en ampèremètre ou en voltmètre.

Utilisation en mode ampèremètre :

Schéma :
 

Utilisation en mode voltmètre :

Schéma :

c. Application

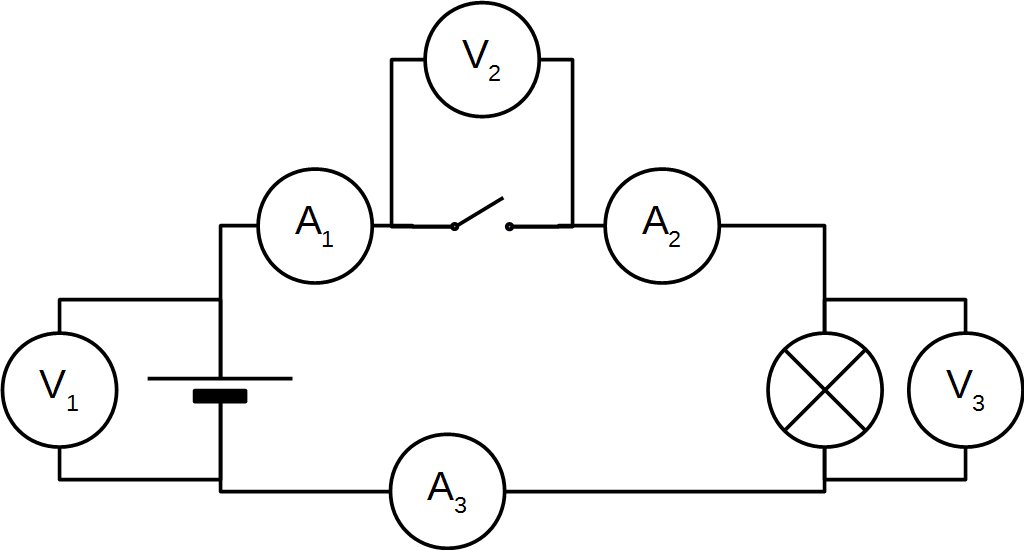
Nous allons utiliser le multimètre pour mesurer les différentes valeurs que prennent tension et intensité dans un montage simple.

Il est possible de mesurer la tension et l'intensité en 3 points du circuits respectivement V1, V2, V3 et A1, A2, A3, et cela lorsque l'interrupteur est ouvert et lorsqu'il est fermé.
Voici les valeurs obtenues par un des groupes :

Interrupteur fermé Interrupteur ouvert
V1 = 3.96 V A1 = 0.12 A V1 = 4.17 V A1 = 0 A
V2 = 0.1 V A2 = 0.12 A V2 = 4.17 V A2 = 0 A
V3 = 3.88 V A3 = 0.12 A V3 = 0 V A3 = 0 A

2- Les lois de l'électricité

a) Activité

Cliquez ici pour télécharger l'activité.

b) Dans un circuit en dérivation

Tension dans un circuit en dérivation

On remarque que les tensions aux bornes des différents dipôles ont toutes les mêmes valeurs, par conséquent :

Dans un circuit en dérivation la tension aux bornes des différents dipôles est égale à la tension aux bornes du générateur.

 
Intensité dans un circuit en dérivation

On remarque que l'intensité sortant de la pile (0.29 A) est égale à l'incertitude de mesure près à l'intensité entrant dans la première lampe ajoutée à celle entrant dans la seconde lampe (0.07 A + 0.21 A = 0.28 A), donc :

Dans un circuit en dérivation l'intensité sortant de la pile est égale à la somme des intensités entrant dans les différentes branches du circuit.

 

c) Dans un circuit en série

Tension dans un circuit en série

On remarque que la tension aux bornes de la pile (4.21 V) est égale à la somme des tensions aux bornes des deux lampes (3.47 V + 0.74 V = 4.21 V), donc :

Dans un circuit en série, la tension aux bornes du générateur est égale à la somme des tensions aux bornes des autres dipôles.

 
Intensité dans un circuit en série

On remarque que les intensités entrant dans les différents dipôles ont toutes les mêmes valeurs, par conséquent :

Dans un circuit en série, l'intensité est la même en tout point du circuit.

 

II- Un nouveau dipôle : la résistance

1. Caractéristique courant-tension

Est-il possible dans un dipôle de faire un lien entre l'intensité qui le parcourt et la tension à ses bornes ? Cela permettrait de gagner du temps en ne faisant qu'une seule mesure !

Avec une lampe :

Tension (V) 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
Intensité (mA) 0 29 39 48 56 63 69 75 81 86 91 96 101

Avec une résistance :

Tension (V) 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
Intensité (mA) 0 8 15 22 30 37 45 52 60 67 75 82 90

Avec une DEL :

Tension (V) 0 0.3 0.6 0.9 1.2 1.5 1.8 2.1 2.4 2.7 3 3.3 3.6
Intensité (mA) 0 0 0 0 0 0 0 0 0.01 1.4 5.6 15.8 36.5
 

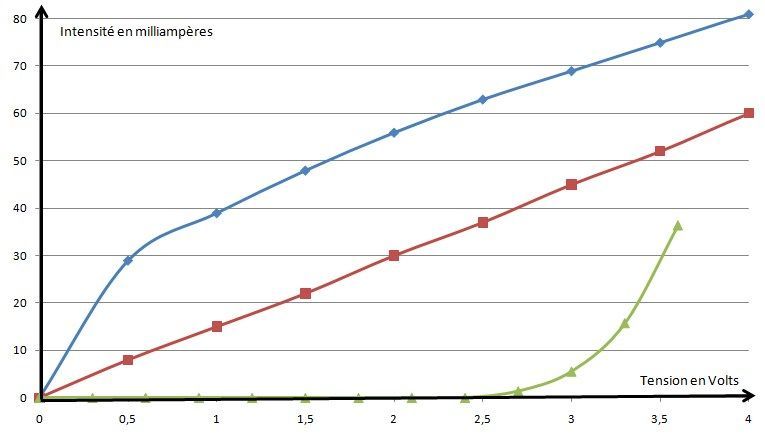
Relation entre la tension et le courant dans 3 différents dipôles
Légende :
- en bleu, la lampe
- en rouge, la résistance
- en vert, la DEL

On remarque que seuls les points de mesure correspondant à la résistance sont alignés sur une droite passant par l'origine du graphique : cela signifie qu'il y a une relation de proportionnalité. On peut donc dans une résistance trouver l'intensité qui la parcourt en fonction de la tension à ses bornes en multipliant par un coefficient.
 

2. Unité

Une résistance se mesure en ohms ().
La valeur de cette résistance représente le coefficient de proportionnalité existant entre l'intensité traversant la résistance et la tension à ses bornes, ce que l'ont peut écrire de cette façon :

U = R x I U est la tension aux bornes de la résistance en Volts (V).
R est la valeur de la résistance en ohms ().
I la valeur de l'intensité qui traverse la résistance en Ampères (A).

On peut utiliser cette formule pour calculer U, R ou I :
1- on connait la résistance R et l'intensité I et on veut calculer la tension : U = R x I
1- on connait la résistance R et la tension U et on veut calculer l'intensité : I = U / R
1- on connait l'intensité I la tension et on veut calculer la résistance : R = U / I

3. Mesure d'une résistance

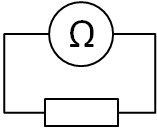
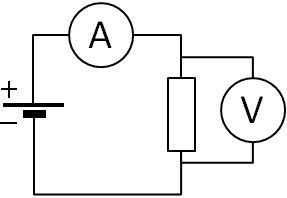
Il est possible de mesurer la valeur d'une résistance en utilisant un multimètre en position ohmmètre.
 
Il est également possible de la calculer en utilisant un générateur, un voltmètre et un ampèremètre.
On mesure la tension (en volts) et l'intentisté (en ampères) puis l'on applique la formule :
U = R x I
 

Exemples :

R1 R2
Tension 3.7 V 4.3 V
Intensité 0.41 A 8.06 mA
Calcul de R1 :
R1 = 3.7 / 0.41 = 3

Calcul de R2 :
Il faut convertir 8.06 mA = 0.00806 A.
R2 = 4.3 / 0.00806 = 533

Comment lire la valeur d'une résistance ?

La plupart des résistances du commerce possèdent un code couleur qui permet de lire leur valeur.
Ce code est composé de 4 anneaux :
    - Les deux premiers sont des chiffres qui s'assemblent pour former un nombre
    - Le troisième est un multiplicateur
    - Le dernier, généralement doré, représente la précision de la résistance (5%).

Voici le code :
Couleur : 1er et 2ème chiffre Multiplicateur
Noir
Marron
Rouge
Orange
Jaune
Vert
Bleu
Violet
Gris
Blanc		 0
1
2
3
4
5
6
7
8
9		 x 1
x 10
x 100
x 1 000
x 10 000
x 100 000
x 1 000 000
x 10 000 000
x 100 000 000
x 1 000 000 000
Exemples d'application :


bleu - gris - marron - or = 6 8 x 1 = 68


rouge - violet - vert - or = 2 7 x 100 000 = 2 700 000 = 2.7 M

Entraînez-vous !

 
 

Réponse :
Sa résistance en ohms est :  .

4. Utilisations des résistance

a) Protéger un dipôle

Certains dipôles (comme les DEL) sont très sensibles à la tension à leur bornes. On l'a vu lors de la première manipulation, dès que la DEL commence à s'allumer, l'intensité qui la traverse augmente très vite : si le générateur n'est pas très précis (s'il fournit 2.7V au lieu de 2.3V par exemple) une DEL seule risque facilement d'être détruite !

En mettant en série une DEL et une résistance qui limite le courant, cela permet d'éviter de détériorer la DEL.
Exemple : une DEL rouge qui s'allume à environ 2V et grille à 2.7V pourra fonctionner sur un générateur délivrant 7V avec une résistance de 100 .

b) L'effet Joule

  1. Qu'est-ce que l'effet Joule ?
    2. L'effet joule correspond à un dégagement de chaleur lors du passage d'un courant électrique dans un conducteur.
  2. Comment un fusible protège-t-il les installations électriques d'une trop grande intensité ?
    3. Un fusible est un conducteur calibré pour supporter le passage d'une certaine intensité. Au-delà de cette intensité, l'effet Joule est tel que le fusible fond. Le courant ne peut plus passer et isole la machine ayant un problème électrique du reste du circuit et empêche celui-ci d'être détruit.
  3. Cite d'autres exemples d'appareils qui utilisent l'effet Joule.
    4. Les appareils utilisant l'effet Joule sont en général des appareils de chauffage : le chauffage électrique ou la bouilloire par exemple.

c) D'autres types de résistances

  1. 1- Quelles sont les trois familles de "résistances" particulières décrites dans ce document ?
    2. Les trois familles de résistances sont :
    - les potentiomètres dont on peut faire varier manuellement la résistance
    - les thermistances dont la résistance varie en fonction de la température
    - les photorésistances dont la résistance varie en fonction de la lumière.
  2. Comment un potentiomètre permet-il de modifier l'intensité du courant qui le traverse ?
    3. Un cadrant permet généralement de laisser passer le courant à travers une plus ou moins grande partie du conducteur, ce qui permet d'avoir une plus ou moins grande résistance.
  3. Dans quel but utilise-t-on les thermistances ?
    4. Les thermistances sont un moyen simple de mesurer électriquement la température. On les utilise donc pour contrôler la température des chauffe-ballon ou comme thermomètre électronique.
  4. Comment évolue la valeur d'une photorésistance quand elle reçoit plus de lumière ?
    5. La résistance d'une photorésistance peut aller de quelques ohms en pleine lumière à plusieurs centaines de millions d'ohms dans l'obscurité.

5. Exercices autour de la résistance

a) Relation courant/tension

Pierre a mesuré la tension aux bornes d'une résistance, et de deux autres dipôles ainsi que l'intensité qui les parcourait.

Il a récapitulé les résultats dans 3 tableaux différents.
Malheureusement Pierre a oublié de noter lequel de ces trois dipôle était la résistance.

Pourrais-tu aider Pierre ? Retrouve pour lui lequel des dipôles 1,2 ou 3 est la résistance et explique lui les raisons de ton choix.
Tension (V) 3 4 7
Intensité (mA) 1 6 13
Dipôle 1

Tension (V) 3 4 7
Intensité (mA) 1 2 3
Dipôle 2

Tension (V) 3 4 7
Intensité (mA) 4.5 6 10.5
Dipôle 3

b) Quelques conversions

Convertir les valeurs suivantes

multiple  25 mA    mV    1375 mV    200 µA    100kV    µA    55 M  
Unité SI   A    3 V     V     A     V    0.000 026 A      

c) Mesurer la valeur d'une résistance

Clarisse et Paul mesurent la valeur d'une résistance à l'aide d'un voltmètre et d'un ampèremètre. Ils relèvent les valeurs suivantes :
Tension = 4.3 V, Intensité = 3.25 mA.

a) Faire le schéma du montage réalisé par Clarisse et Paul.
b) Donner la valeur de la résistance mesurée.
c) Quel autre montage auraient pu utiliser Clarisse et Paul pour mesurer la résistance ? En proposer un schéma.

d) Code couleur

En utilisant le code couleur, trouver la valeur des résistances suivantes :

  • vert, noir, noir, or
  • rouge, orange, marron, or
  • vert, bleu, rouge, or
  • bleu, blanc, rouge, or
  • or, orange, blanc, vert

e) Utilisation de U = R x I

Compléter le tableau suivant :

U 4.5 V 3.6 V 17 V
I 0.00035 A A 0.032 A 3.4 mA A
R 2000 35 470 370 k
Previous page: De l'air qui nous entoure à la molécule Next page: L'eau dans notre Environnement