Langages et programmation
I- Introduction
Il est très souvent possible d'écrire des algorithmes totalement différents pour effectuer une tâche, résoudre un problème.Comment comparer ces différentes solutions si elles donnent le même résultat ?
Le but de cette partie va être d'aborder la notion de complexité : ce qu'elle signifie et comment on la détermine.
Enfin, nous verrons comment s'assurer qu'un algorithme simple donnera toujours une solution correcte.
Afficher Partie 1 : Complexité
Cacher Partie 1 : Complexité
II- Algorithmes de recherche
Cliquez sur Fiche algorithmes01.pdf pour récupérer l'énoncé du TD.
Travail préalable : créer une fonction alea_liste(n) qui retourne une liste de n nombres entiers aléatoires xi, avec 0 ≤ xi ≤ n dans le second cas
Affiche l'algorithme
Cacher l'algorithme
Il est possible d'écrire cette fonction en une seule ligne, mais l'import de la fonction randint(début,fin) présente dans le module random est nécessaire.from random import randint def alea_liste(n): return [randint(0,n) for i in range(n)]
1) Algorithmes de parcours d'un tableau
Pour les exercices suivants, on utilisera la liste :
a. Écrire une fonction indice(liste,valeur) qui retourne l’indice de la premiere occurrence de valeur dans liste.
Exemple : indice(test,36) doit retourner la valeur 7, car test[7]=36.
test=[19, 16, 28, 26, 50, 16, 0, 36, 1, 45, 38, 27, 37, 16, 45, 41, 3, 19, 49, 43, 19, 44, 40, 23, 33, 25, 30, 38, 28, 49, 31, 37, 8, 48, 34, 12, 25, 6, 37, 23, 32, 36, 44, 45, 36, 29, 17, 11, 32, 27]
Exemple : indice(test,36) doit retourner la valeur 7, car test[7]=36.
Affiche l'algorithme
Cacher l'algorithme
def indice(liste,valeur):
for i in range(len(liste)):
if liste[i]==valeur:
return i
return -1
Remarque : il est nécessaire de prévoir le cas où la valeur ne serait pas présente.Il peut être dangereux de retourner False car cela risquerait d'être considéré comme la valeur 0. D'où le choix de retourner un nombre négatif.
Affiche l'algorithme
Cacher l'algorithme
def maximum(liste):
maxi=liste[0]
for i in range(len(liste)):
if liste[i]>maxi:
maxi=liste[i]
return maxi
Affiche l'algorithme
Cacher l'algorithme
def moyenne(liste):
somme=0
for i in liste:
somme+=i
moyenne=somme/len(liste)
return moyenne
III- Evaluation du coût d'un algorithme
1) Mesure expérimentale
Le module time contient une fonction time_ns() retournant le temps écoulé en nanosecondes depuis le 01/01/1970. Il est possible grâce à elle d’évaluer le temps que met une série d’instructions à se réaliser :Affiche l'algorithme
Cacher l'algorithme
from time import time_ns
def bench(fonction,liste):
chrono=time_ns()
fonction(liste)
return time_ns()-chrono
Avec la fonction précédente, on se rend compte qu'il est impossible sur une machine récente de mesurer le temps que met la fonction moyenne(liste) à s'executer !Il est donc nécessaire d'utiliser des listes plus longues pour pouvoir mesurer le temps d'execution :
from time import time_ns
from matplotlib import pyplot as plt
def bench(fonction,l_liste):
liste=alea_liste(l_liste)
chrono=time_ns()
fonction(liste)
return time_ns()-chrono
def bench_fonctions(liste_fonctions,depart,fin,pas,nb_tests=1,labels=False):
k=0
plt.ylabel("temps (ns)")
plt.xlabel("nombre d'éléments")
for fonction in liste_fonctions:
x=[]
y=[]
increment=depart
while increment<fin:
print(increment)
increment+=pas
x.append(increment)
y.append(moyenne([bench(fonction,increment) for i in range(nb_tests)]))
if labels is False:
lab=str(k)
else:
lab=labels[k]
plt.plot(x,y,label=lab)
k+=1
#recherche relation de proportionnalité par méthode des moindres carrés
sum_xi2,sum_xi_yi=0,0
for i in range(len(x)):
sum_xi2 +=x[i]**2
sum_xi_yi +=x[i]*y[i]
a=sum_xi_yi/sum_xi2
plt.plot(x,[a*x[i] for i in range(len(x))])
#fin du tracé de la droite
plt.legend(loc="upper left")
plt.show()
La fonction bench_fonctions va tester une liste de fonction sur un pour des valeurs à définir, puis tracer le graphe du temps de calcul en fonction de la longueur de la liste.bench_fonctions([moyenne],100,1e5,1000,10,["temps de calcul"])on obtient le graphique suivant :
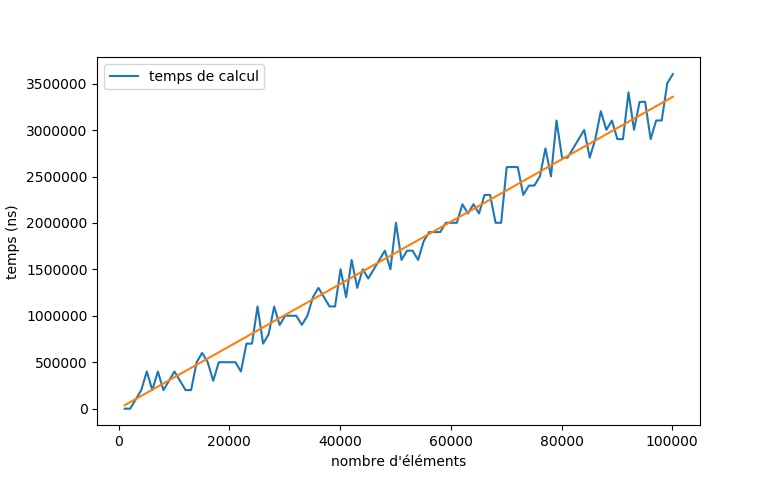
On remarque que si les valeurs sont irrégulières (en effet un ordinateur effectue beaucoup d'autres tâches pendant qu'il exécute un script en python), elles sont cependant en accord avec une relation de proportionnalité : Le temps d'éxécution semble proportionnel au nombre d'éléments présents dans la liste.
2) Vérification
Il n'est pas possible à notre niveau de déterminer exactement combien de temps va prendre le calcul dans le cas de python et d'un ordinateur de bureau, cependant on peut compter le nombre d'opération que fait l'algorithme dans le cas d'une moyenne.→ Pour chaque indice de la liste en entrée, il va ajouter à la variable somme la valeur présente à l'indice. Il réalise cette opération n fois et on suppose qu'elle prend un temps t1. Ensuite, il divise somme par le nombre d'éléments, cela prend un temp t2.
On a donc un temps total de l'ordre de :
ttotal = n × t1 + t2
Si n est suffisamment grand, on peut négliger le temps pris par la division, on retrouve bien un temps proportionnel au nombre d'éléments.
On dit alors que la complexité est en O(n) ("grand O (la lettre o) de n").
On ne connait pas forcément le coefficient de proportionnalité, qui dépend notamment des caractéristiques de la machine, mais on peut affirmer que si un calcul pour n éléments (et n suffisamment grand) a pris un temps t alors pour 2×n éléments, le calcul prendra un temps 2×t.
IV- Algorithmes de tri
Il existe plusieurs façons de trier une liste :-
Le tri par sélection
Celle qui me semble la plus simple est de chercher le maximum d’une liste, puis une fois celui-ci trouvé, échanger sa position avec l’élément en première position de la liste (tri décroissant) ou dernière position (tri croissant).
Affiche l'algorithme
Cacher l'algorithme
En pseudo-code cela donne :procédure tri_selection(tableau t) n ← longueur(t) pour i de 0 à n - 2 min ← i pour j de i + 1 à n - 1 si t[j] < t[min], alors min ← j si min ≠ i, alors échanger t[i] et t[min]
-
Le tri par insertion
on peut aussi prendre consécutivement les éléments de la liste et les remplacer correctement un à un parmi les éléments déjà ordonnés de la liste.Affiche l'algorithme
Cacher l'algorithme
procédure tri_insertion(tableau T) n ← taille(T) pour i de 1 à n - 1 # mémoriser T[i] dans x x ← T[i] # décaler vers la droite les éléments de T[0]..T[i-1] qui sont plus grands que x en partant de T[i-1] j ← i tant que j > 0 et T[j - 1] > x T[j] ← T[j - 1] j ← j - 1 # placer x dans le "trou" laissé par le décalage T[j] ← x
-
Le tri à bulles
On peut enfin balayer progressivement la liste en inversant 1 à 1 chaque couple de nombres consécutivement de façon à ce qu’ils soient dans l’ordre de rangement, et cela jusqu’à ce que la liste soit ordonnée.Affiche l'algorithme
Cacher l'algorithme
procédure tri_insertion(tableau T) n ← taille(T) pour i de 1 à n - 1 # mémoriser T[i] dans x x ← T[i] # décaler vers la droite les éléments de T[0]..T[i-1] qui sont plus grands que x en partant de T[i-1] j ← i tant que j > 0 et T[j - 1] > x T[j] ← T[j - 1] j ← j - 1 # placer x dans le "trou" laissé par le décalage T[j] ← x
Implémenter ces 3 algorithmes en python
Ces trois algorithmes retournent une liste correctement ordonnée, comment les classer ?Affiche l'algorithme
Cacher l'algorithme
def tri_selection(liste):
for i in range(len(liste)):
maxi=liste[0]
indice=0
for j in range(len(liste)-i):
if liste[j]>maxi:
maxi=liste[j]
indice=j
liste[indice],liste[len(liste)-i-1]=liste[len(liste)-i-1],liste[indice]
return liste
def tri_insertion(liste):
for i in range(1,len(liste)):
temp=liste[i]
for j in range(1,i):
if liste[i]<liste[j]:
for k in range(i-j):
liste[k+1]=liste[k]
liste[j]=temp
break
return liste
def tri_bulle(liste):
for i in range(len(liste)):
for j in range(len(liste)-i-1):
if liste[j+1]<liste[j]:
liste[j+1],liste[j]=liste[j],liste[j+1]
return liste
bench_fonctions([tri_selection,tri_insertion,tri_bulle],125,2.5e3,125,10,["tri par sélection","tri par insertion","tri à bulles"]).
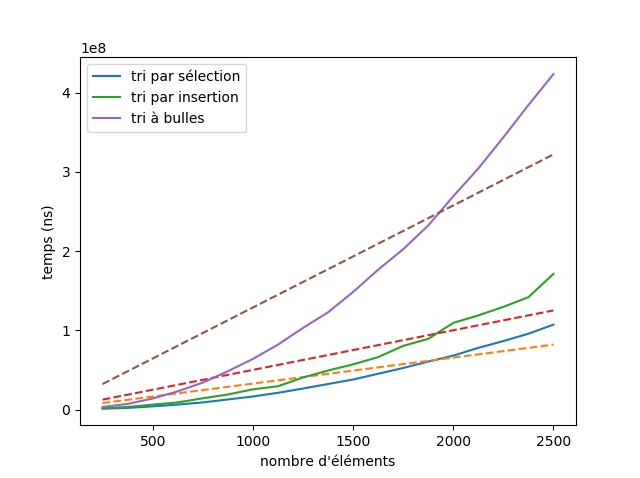
Le tri à bulles est (beaucoup) plus lent que les deux autres méthodes !
On remarque également que le temps de calcul n'est plus proportionnel au nombre d'éléments de la liste mais augmente plus vite que le nombre d'éléments.
Pour voir si ce temps augmente bien en fonction de n2, il suffit de changer l'axe vertical : au lieu de tracer t en fonction de n, on peut tracer √t en fonction de n.
Dans cette représentation, les relations proportionnelle à n2 sont visibles :
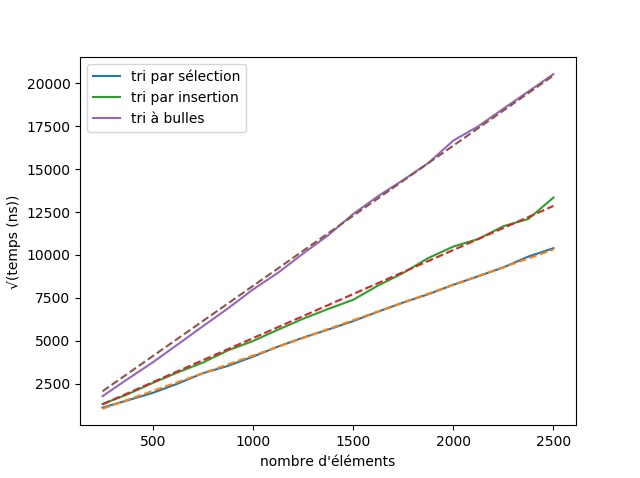
Même si le tri à bulles est le moins efficace, ces trois tris ont une complexité en O(n2)
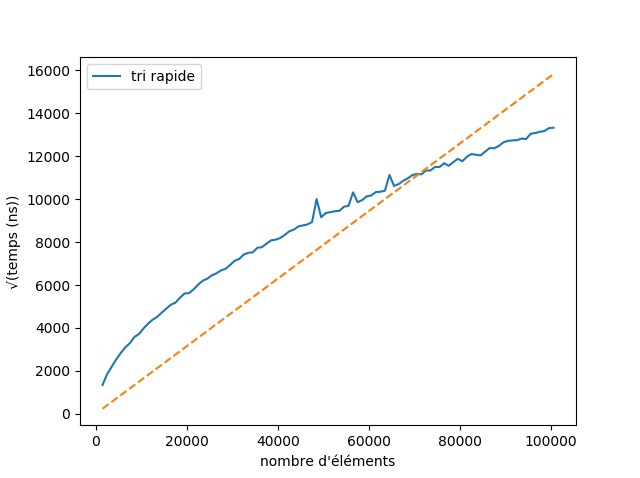
Remarque :Ces 3 tris ne sont pas considérés commes efficaces, il existe des tris bien plus rapides, comme le tri fusion ou le tri rapide dont la complexité est inférieure à O(n2).
Afficher Partie 2 : Mini-Projets
Cacher Partie 2 : Mini-Projets
Le but de ces projets est d'aborder la manipulation de listes (fondamentale en informatique) au travers d'exemples afin de rendre ces manipulations plus compréhensibles.1) Le morpion
Le morpion est un jeu à 2 joueurs sur une grille de 3 × 3 cases.Chaque joueur place tour à tour une marque dans une case vide, le premier à aligner 3 de ses marques a gagné.
Le fichier suivant contient un script avec l'ossature du programme ainsi que les directives pour le remplir :
cliquez ici !
Un tableau est créé : il s'agit d'une liste contenant 3 sous-listes (une par ligne) contenant elles-mêmes 3 valeurs :
grille=[[0 for i in range(3)] for j in range(3)]La grille sera modifiée en cours de jeu avec les valeurs suivantes :
- 0 si vide
- 1 si case remplie par le joueur 1
- 2 si case remplie par le joueur 2
- Décider de la façon dont les joueurs vont indiquer la case choisie.
- Interpréter la réponse du joueur en fonction, et vérifier que la case est jouable, et faire rejouer le joueur si nécessaire jusqu'à ce qu'il propose une case jouable.
- Ajouter une fonction gagne() se chargeant de vérifier que la grille n'est pas dans une situation gagnante.
